バランスのよい形が、「つり合いのとれた図形」ということがなんとなくわかってきました。


次は、飛行機と風車のちがいを考えてみましょう
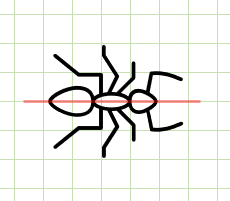
飛行機のつり合い
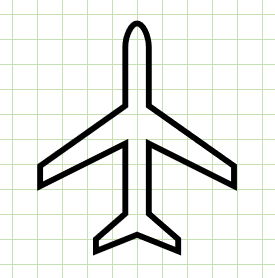

左右の形や長さが同じだから、バランスがいいのだと思います
たしかにそんな感じがします。
しかし、本当に形や長さは同じなのでしょうか?

疑い深いね…折って重ねてみればいいじゃない
いいですね!
では実際に折って重ねてみましょう。
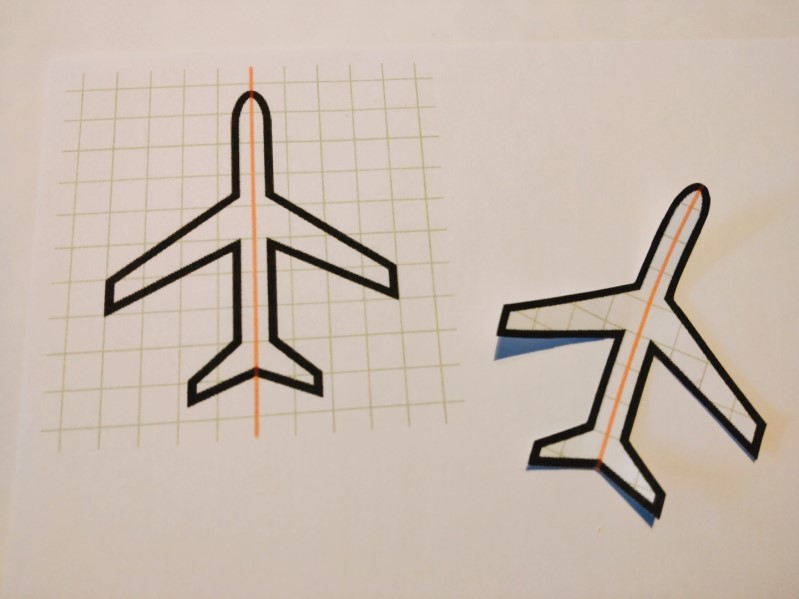

たしかにぴったり重なりました。

おおー!なんかスッキリする~

やっぱり形も長さも同じですね
たしかめられてよかったです!
このようなつり合い方をする図形には名前があります。
折ってぴったり重なる線対称
この飛行機の形は、二つ折りにしたときにぴったり重なるという特徴をもっています。

1本の直線を折り目にして二つ折りにしたとき、両側の部分がぴったり重なる図形を、線対称な図形といいます。
折り目となったのは赤い直線でしたね。
その直線にも名前があります。

ぴったり重なるように折ったときの折り目となる直線を、対称の軸といいます。

名前はわかった!
ちょっと気になったんだけど、これ↓って線対称なのかな?
対称の軸はどうなりそうですか?

ここで折れば重なると思うけど…横になっちゃうから、いいのかなと思って
はい、対称の軸はたてじゃなくて横でもいいのです。
もちろんななめでも。
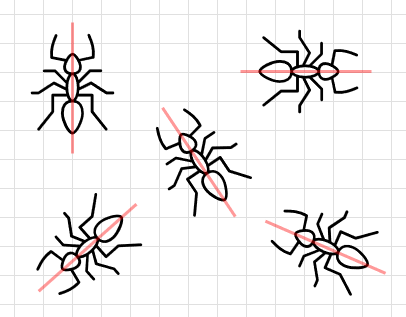
とにかく、対称の軸で二つ折りにした時にぴったり重なるということが重要です。

たしかに、どっちを向いていても形は同じだし、対称の軸で折れば重なりますね
線対称な図形の性質を調べてみよう
すべての図形がいつでも折って確かめられるわけではありません。
しかし、性質を知っていれば、折らなくても線対称かどうか確かめることができます。
シンプルな図形で調べてみましょう。
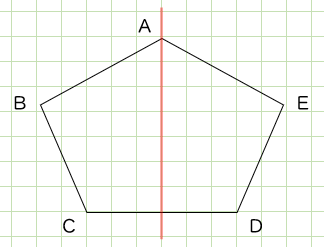
これも線対称な図形です。

線対称な図形で、二つ折りにしたときに重なり合う辺、角、点を、それぞれ対応する辺、対応する角、対応する点といいます。
辺ABに対応する辺は、辺AE。
辺BCに対応する辺は、辺ED。
角Eに対応する角は、角B。
角Dに対応する角は、角C。
となります。
対称の軸で折ったら重なるわけですから、対応する辺の長さや角の大きさは同じです。

角Aとか辺CDは?
角Aは、対称の軸で半分に分けられています。
★の角が対応することになりますね。
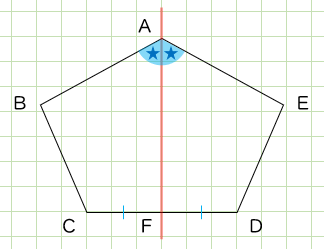
辺CDも、折ると重なります。
対称の軸と交わる点をFとして考えてみましょう。

辺CFに対応するのが辺DFということですね

ところで、対応する「頂点」じゃないの?
するどいですね。
頂点も点ですが、図形には頂点以外にとんでもなくたくさんの点があるのです。
例えば、下の点Gに対応するのは…
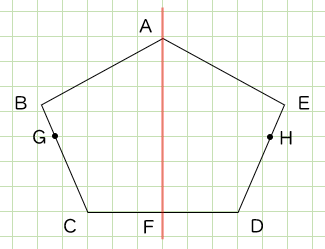

点Hということですか
たしかに辺の上のどこにでも点がありそうですね
図形の中にもあるのです。
さて、点Hはどうやって決まっているのでしょう?

点Gの真横にあるって感じ
そうですね。
「真横」というのがどういうことかというと…
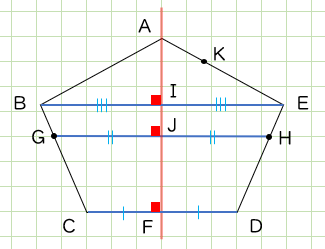

おー!
対応する点を結んだんだ
平行でいい感じだね
対応する点を結ぶと、対称の軸と垂直に交わります。
だから、平行になるのですね。

4年生で学習しましたね
直線BIと直線EI、直線GJと直線HJも、それぞれ同じ長さになります。
では、点Kに対応する点はどこになるか…?
考えてみてくださいね。
線対称な図形をかいてみよう
続きをかいて、線対称な図形にしてみましょう。
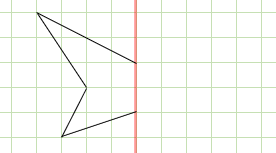

あ!なんかかけそう!
蝶みたいな形になりそうだね
かく前に予想するのはいいですね。
いきなり線を引き始めてもかけそうですが、性質を活用し、対応する点を見つけてかいてみます。
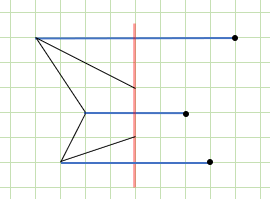
それぞれの点から対称の軸と垂直になるように直線を引き、対称の軸から同じ長さのところに点をうちます。

マスが正方形だから、かきやすいですね
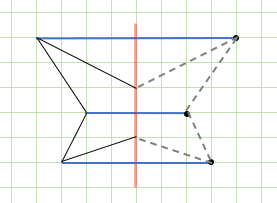
決まった点をつなげば、できあがり。

つり合いとれていますね!
オリジナルの図形もかけますよ。
まずは対称の軸をかきましょう。

どちらか半分をかいてから、対応する点を見つけてつないでいきましょう。

いろんな形がかけそう!


